Three Common Sorting Algorithms with JavaScript

In this article, we’ll learn about three common sorting algorithms: bubble sort, selection sort, and merge sort. We’ll explore what they’re useful for, as well as how to implement them in JavaScript.

Introduction to sorting

When we think about sorting, we think about the ordering of numbers or ordering strings alphabetically, or perhaps, in the real world, we might think about ordering people – by height, age, etc. In an interview setting, when we’re asked about sorting, we can assume it’s about an array of numbers. Usually, we’ll need to write some code to take these numbers, and sort them from least to greatest.

[3, 8, 5, 9, 1, 2] -> [1, 2, 3, 5, 8, 9]

If you’re a JavaScript developer, the sort() array method might come to your mind.

console.log([3, 8, 5, 9, 1, 2].sort());
// [ 1, 2, 3, 5, 8, 9 ]

The underlying algorithm for this built-in sort() method is implemented differently depending on which browser you are using. Browsers have different JavaScript engines, which is a way to execute JavaScript code. For example, Chrome uses the V8 engine, while Mozilla Firefox uses SpiderMonkey. Mozilla uses merge sort, while V8 uses Timsort (which we will not discuss in this article.)

How might we implement our own way to sort lists without using the built-in sort() method? That’s what we’re about to find out!

Let’s take a look at some common sorting algorithms.

Time Complexity

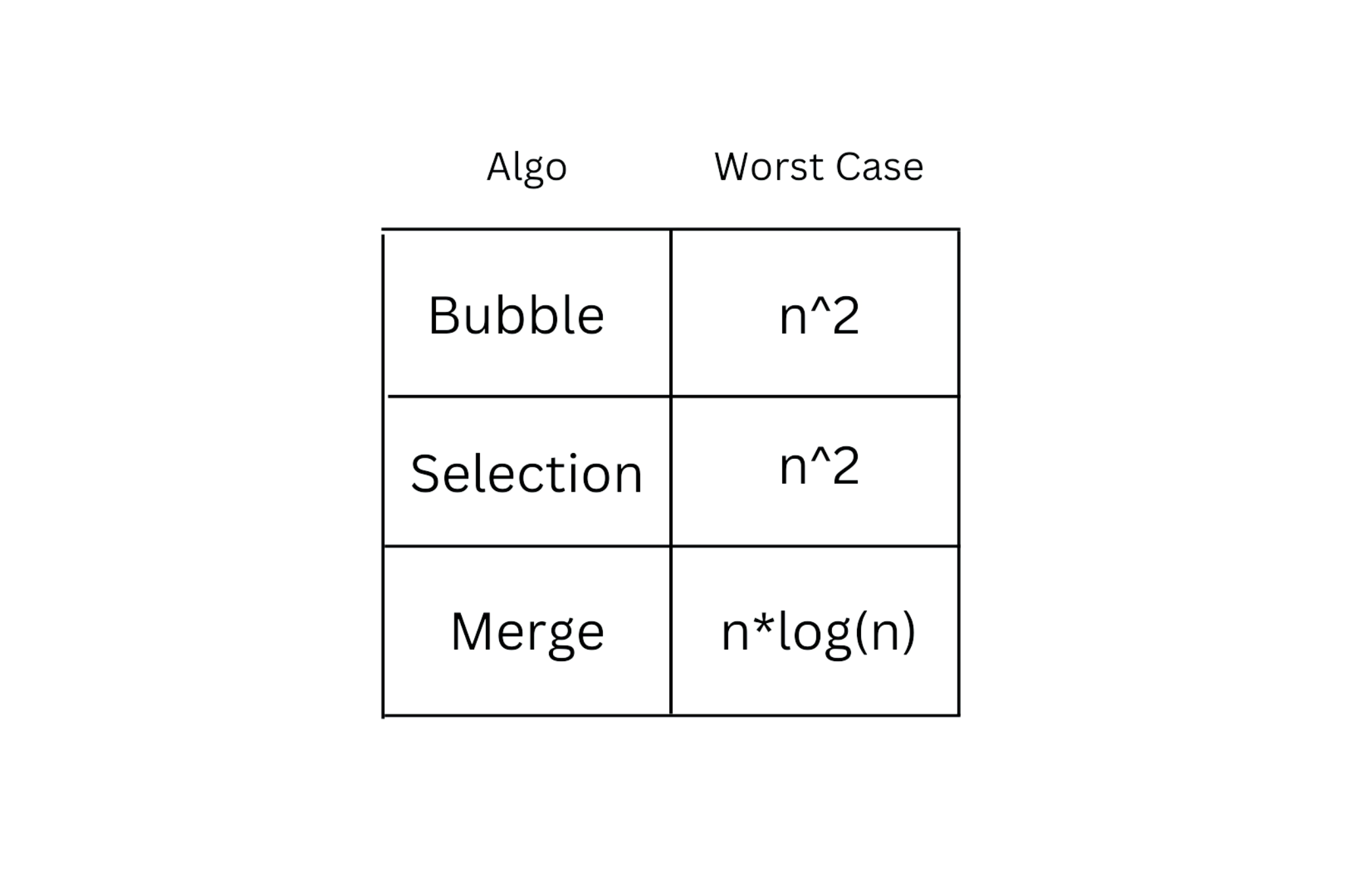
Most common sorting algorithms

Looking at the worst case runtimes, we see that bubble sort and selection sort both have an N^2 runtime. This means that for every additional element that is added to the collection of numbers to be sorted, the algorithm will take significantly more time to run. This means that bubble sort and selection sort would be poor algorithms to use on large data sets. However, if you’re working with smaller data sets and you know it will remain a small data set, there’s nothing wrong with using these algorithms.

In general, when we think about sorting algorithms, we usually assume a worst case scenario of n*log(n).

If you’d like to read more about time complexity, head on over to our article, Runtime Complexity Analysis with JavaScript. But don’t forget to come back!

Bubble Sort with JavaScript

Bubble sort is a sorting algorithm that loops through an input list element by element, comparing the current element with the one after it, and swapping their values if needed. It isn’t actually a useful algorithm except for the purpose of introducing sorting algorithms – due to its simplicity.

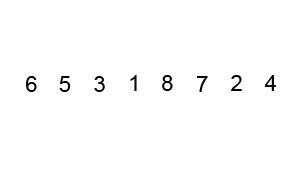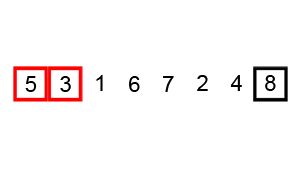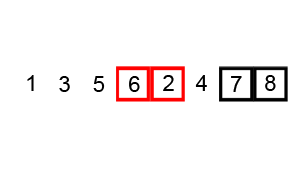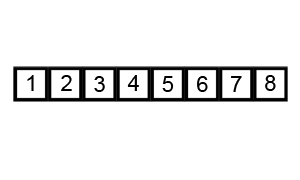
An example of bubble sort. Source: Wikipedia.

Bubble sort is one of the easier methods to solve with JavaScript. We’ll start with the following code:

function bubbleSort(arr) {
  // your code here
}
bubbleSort([3, 4, 9, 5, 1]);

Looking at the input, we see arr, which is short for array. arr will be an array of numbers. As with all of the algorithms we’ll implement in this article, our goal is to sort this array of numbers from least to greatest.

The first step we’re going to want to take is to loop through the array.

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {}
}
bubbleSort([3, 4, 9, 5, 1]);

We’re using a classic for loop in order to get access to both the index and element at every position in the array.

Next, we’re going to want to write an inner for loop, which is going to start looping at index 0, all the way up to the length of the array. The array length is always offset by 1 from the index because arrays are indexed at 0, thus the -1 is going to ensure our code doesn’t iterate where it shouldn’t.

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {}
  }
}
bubbleSort([3, 4, 9, 5, 1]);

Within our for loops, we’re going to want to write some logic that will check the current element and the element next in the array.

if (arr[j] > arr[j + 1]) {
  const lesser = arr[j + 1];
  arr[j + 1] = arr[j];
  arr[j] = lesser;
}

The if statement reads: if the current element at the current index is greater than the next one, which is where we will then swap the values.

Note: The last step doesn’t need a code block of its own. Of course, we’re going to want to return the sorted array. Check the complete implementation below.

The Implementation

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        const lesser = arr[j + 1];
        arr[j + 1] = arr[j];
        arr[j] = lesser;
      }
    }
  }
  // return the sorted array
  return arr;
}

console.log(bubbleSort([3, 4, 9, 3, 1]));

Selection Sort with JavaScript

Selection sort is an in-place comparison sorting algorithm, with an n^2 time complexity, which as we said above, makes it inefficient on large lists of items. It is generally known for its simplicity, and indeed has performance gains over complicated algorithms in specific situations.

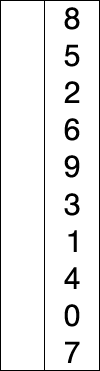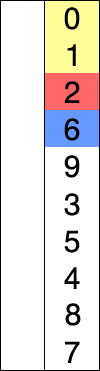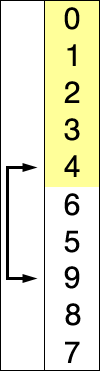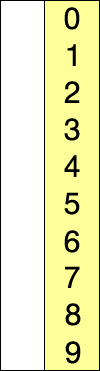
Selection sort animation. Red is current min. Yellow is sorted list. Blue is current item. Source: Wikipedia.

To get an idea of how to implement this algorithm, let’s think about it a bit. We know that we need to compare elements within the array, so we’ll probably need two for loops.

The first step in the algorithm is to run an outer for loop through the entire array:

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {}
}

We also want to declare a variable, indexMin and assign it to i, assuming it is the least element in the array.

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let indexMin = i;
  }
}

Next, we’re going to set up another for loop to validate that indexMin is indeed the least element in the array, but if we see an element that is less, we’re going to record it’s index by storing it in indexMin, as below:

for (let j = i + 1; j < arr.length; j++) {
  if (arr[j] < arr[indexMin]) {
    indexMin = j;
  }
}

The last step of our algorithm is to check whether or not indexMin is equal to i. Remember, we’ve assumed that i is the lowest value above. If they’re not equal, they are going to be swapped.

if (indexMin !== i) {
  let lesser = arr[indexMin];
  arr[indexMin] = arr[i];
  arr[i] = lesser;
}

And that’s it. We have an implementation of selection sort. But don’t forget – the last step is to return the array (arr). See the full implementation below.

The Implementation

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let indexMin = i;

    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[indexMin]) {
        indexMin = j;
      }
    }

    if (indexMin !== i) {
      let lesser = arr[indexMin];
      arr[indexMin] = arr[i];
      arr[i] = lesser;
    }
  }

  return arr;
}
console.log(selectionSort([3, 4, 9, 3, 1]));

Merge Sort with JavaScript

Merge Sort is an algorithm invented by John Von Neumann, who was a brilliant mathematician, physicist, computer scientist, engineer, and polymath. Unlike the two algorithms above, merge sort is an efficient, general-purpose sorting algorithm. It sorts by recursively (we covered recursion a bit in this Fibonacci article) dividing the array into multiple smaller arrays that are sorted and then combines them. We’ll use two separate functions, both serving different purposes.

To put it briefly, merge sort:

1. Divides the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).
2. Repeatedly merges sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.

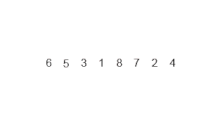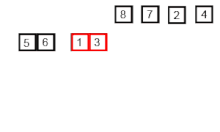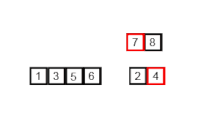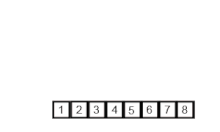
An example of merge sort. Source: Wikipedia.

Tip: Merge sort is one of the must-have algorithms recommended to know by Gayle Laakmann McDowell, author of Cracking the Coding Interview.

Let’s see how to implement merge sort in JavaScript.

Step 1: Merge

The main function, mergeSort() is going to make the recursive calls, so rather than typing this algorithm out line-by-line, we’re going to study each of the functions separately – as the code is tricky and pretty difficult to understand.

merge() is a bit simpler, so let’s take a look at it first.

Notice that merge() accepts two parameters, left and right. left and right are two separate sorted arrays of values. Essentially, the goal of our merge() function is to take these two sorted arrays and merge them together.

You might already be thinking of ways to accomplish this. If you thought of declaring a variable and setting it equal to an empty array, you’re on the right track! Let’s take a look at the merge() function.

// merge()
function merge(left, right) {
  const results = [];

  while (left.length && right.length) {
    if (left[0] < right[0]) {
      results.push(left.shift());
    } else {
      results.push(right.shift());
    }
  }

  return [...results, ...left, ...right];
}

Examine the code block above for a bit. There’s nothing too complex happening here and the function doesn’t contain too much code. Let’s try to run it. Save the code to where you can run it and add console.log(merge([3, 2, 1], [9, 2, 3])) after the function. If you run this, you’ll see that the two arrays, left and right have been merged, returning a single array: [ 3, 2, 1, 9, 2, 3 ].

To get a better understanding of what our code is doing above, these links might be useful to you:

• .push() method
• .shift() method
• Spread Syntax

Step 2: MergeSort

So far we have implemented one part of our algorithm. It’s time to complete it by implementing mergeSort().

After you have taken some time to understand the merge() function, take a look at the function below, mergeSort(). This is where things are going to get confusing.

// mergeSort()
function mergeSort(arr) {
  if (arr.length === 1) {
    return arr;
  }

  const center = Math.floor(arr.length / 2);
  const left = arr.slice(0, center);
  const right = arr.slice(center);

  return merge(mergeSort(left), mergeSort(right));
}

First, let’s actually test our code out.

console.log(mergeSort([4, 3, 2, 1])) -> [ 1, 2, 3, 4 ]

It works, but what’s going on?

If we slow down and think about it for a little, we’ll come to see that we must take the arr parameter, split it into two, and then pass it to the merge() function (but only when there’s nothing left to split).

Let’s see what those three variables are doing.

const center = Math.floor(arr.length / 2);
const left = arr.slice(0, center);
const right = arr.slice(center);

console.log(center, left, right);
// 2 [ 4, 3 ] [ 2, 1 ]
// 1 [ 4 ] [ 3 ]
// 1 [ 2 ] [ 1 ]

So, as we’ve said above, our code should split the array in half, until it cannot do that anymore, in which the array will be passed into the merge() function. As we only have 4 elements in the array, it will be split once in the middle, then again on both the left and right. We will be left with [4, 3] and [2, 1], which will be passed into merge as merge([4, 3], [2, 1]).

Recursion is quite confusing on its own, we know this algorithm might leave you scratching your head. But take some time to experiment with it. Study it, even memorize it.

The Implementation

function mergeSort(arr) {
  if (arr.length === 1) {
    return arr;
  }

  const center = Math.floor(arr.length / 2);
  const left = arr.slice(0, center);
  const right = arr.slice(center);

  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  const results = [];

  while (left.length && right.length) {
    if (left[0] < right[0]) {
      results.push(left.shift());
    } else {
      results.push(right.shift());
    }
  }

  return [...results, ...left, ...right];
}
console.log(mergeSort([3, 4, 9, 3, 1]));

Conclusion

This was a long article and if you’ve made it this far, pat yourself on the back! We explored three different sorting algorithms and wrote them in JavaScript. There are a lot of other sorting algorithms that you might want to check out, such as quicksort, insertion sort, and many more. You can explore them on other areas of the web. You can also subscribe to our newsletter over on the right to stay updated as we write more about algorithms in JavaScript.

Recommended Resources

• Grokking Algorithms (Book)
• Algorithms Specialization (Coursera)
• Runtime Complexity Analysis with JavaScript (Article)

Full Disclosure: this post contains affiliate links. However, we only recommend books or products (courses) that we have personally read or used. We may receive a (very) small commission if you purchase any of the books or courses from this list (at no additional cost to you).